解答例 1

$\mathbb{Z}$ 準同型 $$ f:\mathbb{Z}\rightarrow\mathbb{Z}/m\mathbb{Z}\otimes_{\mathbb{Z}}\mathbb{Z}/n\mathbb{Z}, \quad x\mapsto (1+m\mathbb{Z})\otimes(x+n\mathbb{Z}) $$ を考える. 任意の $z\in\mathbb{Z}/m\mathbb{Z}\otimes_{\mathbb{Z}}\mathbb{Z}/n\mathbb{Z}$ に対して, $$ z=\sum_{i=1}^{r}c_i((x_i+m\mathbb{Z})\otimes(y_i+n\mathbb{Z})), \quad c_i,x_i,y_i\in\mathbb{Z} $$ とおくと, \begin{align*} z &= \sum_{i=1}^{r}c_i((1+m\mathbb{Z})\otimes(x_iy_i+n\mathbb{Z})) \\ &= \sum_{i=1}^{r}(1+m\mathbb{Z})\otimes(c_ix_iy_i+n\mathbb{Z}) \\ &= (1+m\mathbb{Z})\otimes(w+n\mathbb{Z}),\quad w=\sum_{i=1}^rc_ix_iy_i\in\mathbb{Z} \end{align*} より, $f(w)=z$ となる. よって, $f$ は全射である.

$d=\gcd(m,n)$ より, ある $s$, $t\in\mathbb{Z}$ が存在して, $d=ms+nt$ と表せる. このとき, 任意の $y\in\mathbb{Z}$ に対して, \begin{align*} f(dy) &= (1+m\mathbb{Z})\otimes(dy+n\mathbb{Z}) \\ &= (1+m\mathbb{Z})\otimes((msy+nty)+n\mathbb{Z}) \\ &= (1+m\mathbb{Z})\otimes(msy+n\mathbb{Z}) + (1+m\mathbb{Z})\otimes(nty+n\mathbb{Z}) \\ &= (msy+m\mathbb{Z})\otimes(1+n\mathbb{Z}) + (1+m\mathbb{Z})\otimes(nty+n\mathbb{Z}) \\ &= 0. \end{align*} よって, $d\mathbb{Z}\subseteq\mathrm{Ker}(f)$.

写像 $$ \mathbb{Z}/m\mathbb{Z}\times\mathbb{Z}/n\mathbb{Z}\rightarrow\mathbb{Z}/d\mathbb{Z}, \quad (x+m\mathbb{Z}, y+n\mathbb{Z})\mapsto xy+d\mathbb{Z} $$ は $\mathbb{Z}$ 上双線型なので, テンソル積の普遍性により, $\mathbb{Z}$ 準同型 $$ g: \mathbb{Z}/m\mathbb{Z}\otimes_{\mathbb{Z}}\mathbb{Z}/n\mathbb{Z}\rightarrow\mathbb{Z}/d\mathbb{Z}, \quad (x+m\mathbb{Z})\otimes(y+n\mathbb{Z})\mapsto xy+d\mathbb{Z} $$ が存在する. $x\in\mathrm{Ker}(f)$ とすると, $f(x)=0$ なので, $$ x+d\mathbb{Z} = g((1+m\mathbb{Z})\otimes(x+n\mathbb{Z})) = g\circ f(x) = 0. $$ すなわち, $x\in d\mathbb{Z}$. ゆえに, $\mathrm{Ker}(f)\subseteq d\mathbb{Z}$ となる. したがって, $\mathrm{Ker}(f)=d\mathbb{Z}$. 準同型定理により, $\mathbb{Z}$ 上の同型 $$ \mathbb{Z}/d\mathbb{Z}\cong\mathbb{Z}/m\mathbb{Z}\otimes_{\mathbb{Z}}\mathbb{Z}/n\mathbb{Z}, \quad x+d\mathbb{Z}\mapsto (1+m\mathbb{Z})\otimes(x+n\mathbb{Z}) $$ が得られ, $g$ がその逆写像になる.

解答例 2

短完全系列 $$ 0 \rightarrow \mathbb{Z} \stackrel{[m]}{\rightarrow} \mathbb{Z} \stackrel{\pi}{\rightarrow} \mathbb{Z}/m\mathbb{Z} \rightarrow 0. $$ に対して, テンソル積の右完全性より $$ \mathbb{Z}\otimes_{\mathbb{Z}}\mathbb{Z}/n\mathbb{Z} \stackrel{[m]\otimes \mathbb{Z}/n\mathbb{Z}}{\longrightarrow} \mathbb{Z}\otimes_{\mathbb{Z}}\mathbb{Z}/n\mathbb{Z} \stackrel{\pi\otimes \mathbb{Z}/n\mathbb{Z}}{\longrightarrow} \mathbb{Z}/m\mathbb{Z}\otimes_{\mathbb{Z}}\mathbb{Z}/n\mathbb{Z} \rightarrow 0 $$ も完全系列である. ここで, $[m]$ は $m$ 倍写像, $\pi$ は自然な準同型である. また, $\mathbb{Z}$準同型 $f:M\rightarrow N$ と $\mathbb{Z}$ 加群 $W$ に対して, $f\otimes W$ を $$ f\otimes W: M\otimes_{\mathbb{Z}}W\rightarrow N\otimes_{\mathbb{Z}}W, \quad x\otimes y \mapsto f(x)\otimes y $$ によって定まる $\mathbb{Z}$ 準同型とする. この完全系列から, $$ \mathbb{Z}/m\mathbb{Z}\otimes_{\mathbb{Z}}\mathbb{Z}/n\mathbb{Z} = \mathrm{Im}(\pi\otimes\mathbb{Z}/n\mathbb{Z}) \cong \frac{\mathbb{Z}\otimes_{\mathbb{Z}}\mathbb{Z}/n\mathbb{Z}}{\mathrm{Ker}(\pi\otimes\mathbb{Z}/n\mathbb{Z})} = \frac{\mathbb{Z}\otimes_{\mathbb{Z}}\mathbb{Z}/n\mathbb{Z}}{\mathrm{Im}([m]\otimes\mathbb{Z}/n\mathbb{Z})}. $$

一方, $\mathbb{Z}$ 加群としての同型 $$ \varphi: \mathbb{Z}\otimes_{\mathbb{Z}}\mathbb{Z}/n\mathbb{Z}\rightarrow\mathbb{Z}/n\mathbb{Z}, \quad r\otimes x\mapsto rx $$ より, 図式

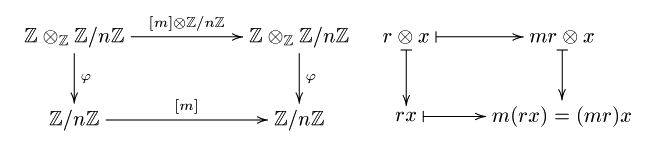
は可換で, \begin{align*} \varphi(\mathrm{Im}([m]\otimes\mathbb{Z}/n\mathbb{Z})) & = \mathrm{Im}(\varphi\circ([m]\otimes\mathbb{Z}/n\mathbb{Z})) = \mathrm{Im}([m]\circ \varphi) \\ & = \mathrm{Im}([m]) = m\cdot \mathbb{Z}/n\mathbb{Z} = d\mathbb{Z}/n\mathbb{Z}. \end{align*} ゆえに, $$ \mathbb{Z}/m\mathbb{Z}\otimes_{\mathbb{Z}}\mathbb{Z}/n\mathbb{Z} = \frac{\mathbb{Z}\otimes_{\mathbb{Z}}\mathbb{Z}/n\mathbb{Z}}{\mathrm{Im}([m]\otimes\mathbb{Z}/n\mathbb{Z})} \cong\frac{\varphi(\mathbb{Z}\otimes_{\mathbb{Z}}\mathbb{Z}/n\mathbb{Z})}{\varphi(\mathrm{Im}([m]\otimes\mathbb{Z}/n\mathbb{Z}))} =\frac{\mathbb{Z}/n\mathbb{Z}}{d\mathbb{Z}/n\mathbb{Z}}\cong\mathbb{Z}/d\mathbb{Z}. $$

最終更新日：2011年11月02日